머신러닝 성능 평가 개념정리

성능평가는 기본적으로 회귀 모델과 분석 모델로 분류해서 평가한다. 이 두 모델은 목표변수 (target)의 유형에 따라 다르다.

 

주요 차이점 요약:

구분	회귀 모델	분류 모델
출력 값	연속적인 값 (예: 실수)	이산적인 값 (예: 클래스/카테고리)
문제 유형	수치 예측 문제 (가격, 수량 등)	카테고리 예측 문제 (스팸/비스팸, 질병 유무 등)
예시	주택 가격 예측, 온도 예측	스팸 메일 분류, 암 진단
평가 지표	MSE, RMSE, MAE, R²	정확도, 정밀도, 재현율, F1 Score
알고리즘	선형 회귀, 다항 회귀, 랜덤 포레스트 회귀	로지스틱 회귀, 의사결정나무, 랜덤 포레스트 분류

 

 

 

회귀 모델 성능 평가 

 

예측 값과 실제 값 간의 차이를 측정하여 모델의 정확도를 평가합니다. 여기 나오는 모든 값들은 작을수록 모델의 성능이 좋다는 것을 의미합니다.

1. MSE (Mean Squared Error, 평균 제곱 오차):

• 정의: 예측 값과 실제 값 사이의 오차를 제곱한 후 평균을 낸 값입니다.
• 공식: 

• 특징: 큰 오차에 대해 패널티를 크게 부여하는 특징이 있어, 모델의 큰 오차에 민감하게 반응합니다. 제곱이기 때문에 오차가 클수록 더 큰 영향을 미치게 됩니다.

2. RMSE (Root Mean Squared Error, 평균 제곱근 오차):

• 정의: MSE의 제곱근을 취한 값으로, MSE보다 직관적으로 이해하기 쉬운 값입니다. 예측 값과 실제 값의 오차를 실제 단위로 표현합니다.
• 공식:

• 특징: MSE와 동일하게 오차가 클수록 더 큰 패널티를 주지만, 제곱근을 취하기 때문에 단위가 예측 변수와 동일해집니다. 직관적으로 오차 크기를 해석하기 쉬운 장점이 있습니다.

3. MAE (Mean Absolute Error, 평균 절대 오차):

• 정의: 예측 값과 실제 값 사이의 절대 오차들의 평균입니다.
• 공식: 

• 특징: 각 오차의 절대값을 평균 내기 때문에 MSE보다 큰 오차에 덜 민감하며, 모든 오차가 동일하게 반영됩니다. 절대값을 사용하므로 오차의 방향성(양/음)에 관계없이 오차 크기만 평가됩니다.

4. MAPE (Mean Absolute Percentage Error, 평균 절대 백분율 오차):

• 정의: 예측 오차의 백분율을 계산하여 평균을 낸 값입니다. MAPE는 예측 값과 실제 값 간의 상대적 차이를 퍼센트로 나타냅니다.
• 공식:

• 특징: 예측 오류를 비율로 표현하므로, 데이터의 스케일에 독립적인 평가를 할 수 있습니다. 하지만 실제 값이 0에 가까울 때 MAPE가 매우 커질 수 있는 단점이 있습니다.

요약

• MSE: 제곱 오차의 평균, 큰 오차에 더 민감.
• RMSE: MSE의 제곱근, 직관적으로 해석 가능.
• MAE: 절대 오차의 평균, 모든 오차를 동일하게 평가.
• MAPE: 오차의 비율을 퍼센트로 표현, 데이터 스케일에 독립적인 평가.

 

5. 결정계수 R²

결정 계수는 예측된 값이 실제 값과 얼마나 일치하는지를 나타내며, 모델이 얼마나 잘 설명하는지를 보여줍니다.

결정 계수(R²) 정의:

결정 계수는 실제 값의 분산 중에서 모델이 설명할 수 있는 비율을 나타냅니다. 쉽게 말해, R² 값이 높을수록 모델이 데이터를 더 잘 설명하고, 낮을수록 모델의 설명력이 부족하다는 의미입니다.

R² 공식:

결정 계수의 공식은 다음과 같습니다.

R2=1−∑(yi−y^i)2∑(yi−yˉ)2R² = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2}R2=1−∑(yi​−yˉ​)2∑(yi​−y^​i​)2​

여기서:

• yiy_iyi​: 실제 값
• y^i\hat{y}_iy^​i​: 예측 값
• yˉ\bar{y}yˉ​: 실제 값의 평균
• ∑(yi−y^i)2\sum (y_i - \hat{y}_i)^2∑(yi​−y^​i​)2: 모델이 설명하지 못한 오차(잔차 제곱합, SSR: Sum of Squared Residuals)
• ∑(yi−yˉ)2\sum (y_i - \bar{y})^2∑(yi​−yˉ​)2: 실제 데이터의 전체 분산(총 제곱합, SST: Total Sum of Squares)

R² 값의 의미:

• R² = 1: 모델이 데이터의 변동을 완벽하게 설명합니다. 즉, 예측 값이 실제 값과 정확히 일치합니다.
• R² = 0: 모델이 데이터를 전혀 설명하지 못합니다. 이는 예측 값이 실제 값의 평균과 동일한 수준임을 의미합니다.
• R² < 0: 모델이 실제 값의 평균을 예측하는 것보다 더 나쁜 예측을 하고 있음을 의미합니다. 이는 모델이 실제 데이터를 잘못 설명하고 있음을 나타냅니다.

결정 계수의 특징:

• R²의 값은 0과 1 사이일 때가 많으며, 1에 가까울수록 모델이 데이터를 잘 설명한다는 것을 의미합니다.
• R²가 0에 가까울수록 모델이 데이터의 변동을 잘 설명하지 못하고 있음을 의미합니다.
• 음수의 R²는 매우 나쁜 모델임을 의미하며, 모델이 데이터의 변동을 설명하는 능력이 거의 없음을 나타냅니다.
• R²는 모델이 얼마나 잘 예측하는지 보여주지만, 오버피팅(overfitting)을 확인하는 지표로는 적합하지 않습니다.

R²의 한계:

• R² 값만으로는 모델의 품질을 완전히 평가하기 어렵습니다. 예를 들어, R²는 오버피팅을 탐지하지 못하며, 특히 변수의 수가 많아지면 R² 값이 무조건 증가할 수 있습니다. 따라서 추가적으로 조정된 결정 계수(Adjusted R²)나 다른 평가 지표(MSE, RMSE 등)를 함께 고려하는 것이 좋습니다.
• 조정된 R² (Adjusted R²): 독립 변수(특징)의 수가 많아지면 R²가 과도하게 높아질 수 있는데, 조정된 R²는 변수의 수를 고려하여 그 영향을 보정한 지표입니다.

예시:

회귀 분석을 통해 주택 가격을 예측하는 모델을 만들었을 때, R² 값이 0.85라고 하면 이 모델은 주택 가격 변동의 85%를 설명할 수 있음을 의미합니다. 나머지 15%는 모델이 설명하지 못하는 변동입니다.

결론:

• R²는 회귀 모델이 데이터를 얼마나 잘 설명하는지를 나타내는 지표입니다.
• 1에 가까울수록 모델의 성능이 좋고, 0에 가까울수록 성능이 낮습니다.
• 하지만 R² 값만으로 모델의 품질을 평가하기에는 부족할 수 있기 때문에 다른 지표들과 함께 사용해야 합니다.

이처럼 결정 계수는 회귀 분석에서 모델의 성능을 빠르게 평가하는 데 유용한 도구입니다.

 

 

 

 

분류 모델 성능 평가

 

류 모델의 성능을 평가하는 다양한 지표들이 있습니다. 각각의 지표는 모델이 예측을 얼마나 잘했는지, 어떤 면에서 잘못했는지를 파악하는 데 도움이 됩니다. 분류 모델에서는 주로 이진 분류(양성/음성)나 다중 클래스 분류 문제에서 사용되는 성능 평가 지표를 사용합니다.

1. 혼동 행렬(Confusion Matrix)

• 정의: 분류 모델의 성능을 평가하기 위해 실제 값과 예측 값을 기준으로 행렬 형태로 나타낸 것.
• 구성:
  • TP (True Positive): 실제 양성이고, 모델이 양성으로 예측한 경우.
  • TN (True Negative): 실제 음성이고, 모델이 음성으로 예측한 경우.
  • FP (False Positive): 실제 음성인데, 모델이 양성으로 잘못 예측한 경우.
  • FN (False Negative): 실제 양성인데, 모델이 음성으로 잘못 예측한 경우.

 

 

2. 정확도(Accuracy)

• 정의: 전체 샘플 중에서 모델이 맞게 예측한 샘플의 비율.
• 공식: 위 이미지 참고​
• 특징: 데이터가 균형 잡혀 있을 때는 유용하지만, 데이터가 불균형할 경우에는 정확도만으로는 성능을 제대로 평가하기 어려울 수 있습니다.

3. 정밀도(Precision)

• 정의: 모델이 양성으로 예측한 것 중에서 실제로 양성인 샘플의 비율.
• 공식: 위 이미지 참고 ​
• 특징: 양성으로 잘못 예측한 경우(False Positive)를 줄이는 것이 중요한 상황에서 유용합니다. 예를 들어, 암 진단 모델에서 암이 없는 사람을 암으로 잘못 진단하는 것을 줄이고 싶을 때 정밀도가 중요합니다.
• 정밀도가 낮을때 발생하는 상황: 암이 아닌데 암이라고해서 불필요한 치료 발생

4. 재현율(Recall, 민감도, Sensitivity)

• 정의: 실제 양성인 샘플 중에서 모델이 양성으로 맞게 예측한 샘플의 비율.
• 공식: 위 이미지 참고 ​
• 특징: 실제 양성을 놓치지 않는 것이 중요한 상황에서 유용합니다. 예를 들어, 질병을 진단하는 모델에서는 질병이 있는 사람을 놓치지 않도록 재현율이 중요합니다.
• 재현율이 낮을때 발생하는 문제: 암인 사람에게 암이 아니라고해서 치료시기를 놓치는 심각한 문제

5. F1 Score (F1 스코어)

• 정의: 정밀도(Precision)와 재현율(Recall)의 조화 평균(Harmonic Mean). 두 성능 지표의 균형을 고려하여 모델의 성능을 평가합니다.
• 공식:

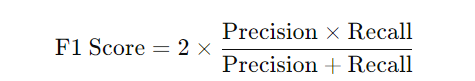
• 특징: 데이터가 불균형할 때 정밀도와 재현율 중 하나에만 치우치지 않고 성능을 평가하는 데 유용합니다.

6. ROC 곡선 (Receiver Operating Characteristic Curve) 및 AUC (Area Under the Curve)

• ROC 곡선: **재현율(Recall)**과 **FPR (False Positive Rate)**의 관계를 시각화한 곡선.
  • FPR (False Positive Rate): 음성을 양성으로 잘못 예측한 비율.
  ​
• AUC (Area Under the Curve): ROC 곡선 아래 면적을 의미하며, 1에 가까울수록 성능이 좋습니다.
  • AUC 값이 0.5에 가까우면 모델이 무작위로 예측한 것과 동일하다는 의미입니다.

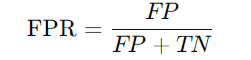
7. 특이도(Specificity)

• 정의: 실제 음성인 샘플 중에서 모델이 음성으로 맞게 예측한 샘플의 비율.
• 공식:

​

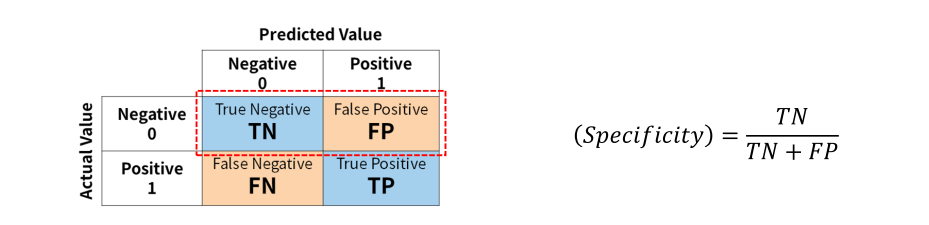
• 특징: 음성을 양성으로 잘못 예측하는 비율을 줄이는 것이 중요한 상황에서 유용합니다.
• 특이도가 낮으면 발생하는 문제: 암이 아닌데 암이라판정나서 불필요한 치료 발생

8. 로지 손실(Log Loss)

• 정의: 모델이 출력한 확률과 실제 값의 차이를 측정하는 손실 함수. 예측한 확률 값이 실제 라벨과 얼마나 차이가 나는지 평가합니다.
• 공식:

.

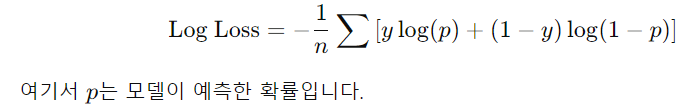
• 특징: 모델이 예측한 확률 값의 신뢰도를 평가하는 데 사용됩니다. 낮을수록 모델 성능이 좋다는 것을 의미합니다.

분류 모델 성능 평가 지표 요약:

지표	정의	특징
정확도	전체에서 맞게 예측한 비율	데이터가 균형 잡혀있을 때 적합. 불균형 데이터에는 부적합.
정밀도	양성으로 예측한 것 중 실제 양성 비율	False Positive를 줄이는 것이 중요할 때 사용.
재현율	실제 양성 중에서 맞게 예측한 비율	False Negative를 줄이는 것이 중요할 때 사용.
F1 스코어	정밀도와 재현율의 조화 평균	정밀도와 재현율 사이의 균형을 평가.
AUC-ROC	ROC 곡선 아래 면적	1에 가까울수록 성능이 좋음.
특이도	실제 음성 중에서 맞게 음성으로 예측한 비율	음성 샘플을 정확히 예측하는 데 초점.
Log Loss	예측 확률과 실제 값의 차이를 평가	확률 예측의 신뢰도 평가. 낮을수록 좋음.

결론:

• 정확도는 직관적인 평가 지표이지만, 데이터 불균형 문제를 다루기에는 적합하지 않습니다.
• 정밀도와 재현율은 중요한 상황에 따라 서로 다르게 사용됩니다. 중요한 것이 False Positive를 줄이는 것인지(False Positive), False Negative를 줄이는 것인지(FN)에 따라 선택합니다.
• F1 Score는 정밀도와 재현율 사이의 균형을 고려해야 할 때 사용합니다.
• AUC-ROC는 모델이 양성과 음성을 얼마나 잘 구분하는지 평가할 때 유용하며, 확률 기반 예측 성능을 평가할 때 많이 사용됩니다.

 

파이썬에서 사이킷런 Scikit-learn 라이브러리에서 제공하는 score함수로 모델성능을 측정하면, 기본적으로

분류문제는 정확도를, 회귀문제는 R² (결젱 계수) 를 반환한다.